


Next:3
Particle identificationUp:ContentsPrevious:1
Introduction
2 Cherenkov ring reconstruction
A typical RICH detector consists of a two-dimensional array (grid) of several
thousand photosensitive cells (pads). During an event a number of Cherenkov
photons produced by a detected particle fall on the pads and form a ring
(or ellipse). In fact, each photon, while registered by the RICH, produces
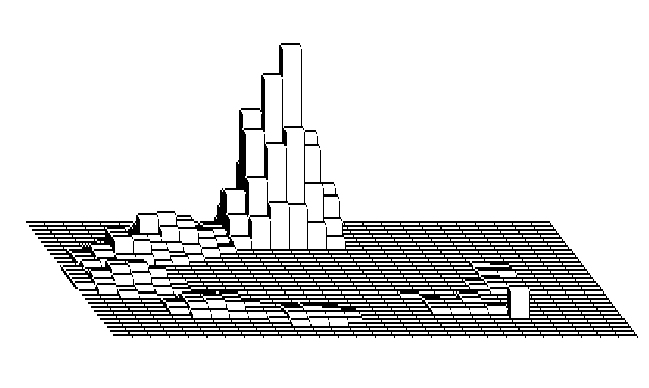
signals in a cluster of adjacent pads near the pad that it hits, see Fig.
1. Thus in order to implement the idea of using the raw data directly,
one should fit a ring to a few pad clusters, each cluster corresponds to
one photon in the ring. This picture sharply contrasts with traditional
fitting models based on the random and independent deviations of measured
points from the circle to be fitted. In our approach, the cells are fixed
but the energy measurements (amplitudes) have random character.
In order to simplify the problem many traditional methods start with
a time-consuming calculation of the hit centers of photons from the raw
data. However, during this hit-extracting procedure one loses the detailed
information of individual pad amplitudes contained in the raw data. Besides,
these procedures are, as usual, inaccurate in the cases of close, overlapping
clusters.
|
 |
|
Figure 1: 3D images of simulated discretized signals of
one Cherenkov ring
|
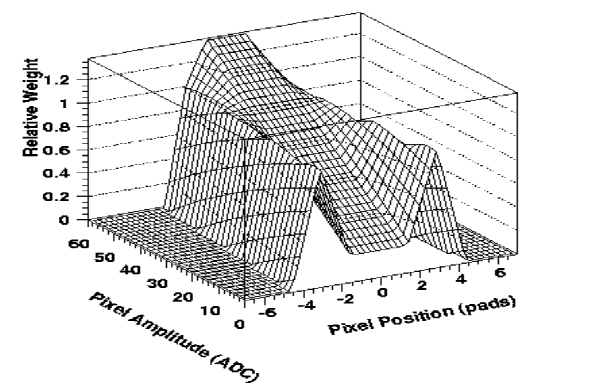
Figure 2: bihorn 2D weight function piecewise linearly approximated
|
Therefore the idea of ring fitting directly from the raw data can potentially
result in faster and more accurate algorithms. In addition, two important
features of RICH detectors must be taken into account: (i) the energy measured
in the pads is discretized and signals both too small and too large are
cut off; (ii) the high occupancy of RICH detectors - the abundance of background
noise and possible presence of two or more overlapping rings. These RICH
data features considerably violate the crucial assumptions of normality
and independence of errors on which the classical least square fit (LSF)
is based. It is assumed that measured point deviations from the observed
ring are normally distributed independent variables with the common
probability density function (p.d.f.) 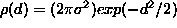 . However, these violations often cause a complete breakdown of the LSF,
since data are contaminated by background measurements with p.d.f. u(d)
and, therefore
. However, these violations often cause a complete breakdown of the LSF,
since data are contaminated by background measurements with p.d.f. u(d)
and, therefore 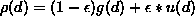 , where
, where 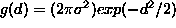 and
and  is the background rate. In such cases the robust weighted least
square procedure
is the background rate. In such cases the robust weighted least
square procedure  works better. The optimal weight function
w(d) for
the uniform background distribution u(d) = const
was derived in our earlier papers [4, 6]
works better. The optimal weight function
w(d) for
the uniform background distribution u(d) = const
was derived in our earlier papers [4, 6]
w(x) =
s-2  1
+
1
+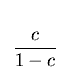
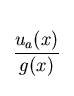
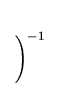
The main problem is to take into account such an essential information
as signal amplitudes measured in each pad.
Corresponding formulae for the optimal weight functions have been derived
in ref. [6] by the maximum likelihood approach.
The formula was obtained for a more general track-finding problem, when
a track passing through a detector hits one of many parallel coordinate
planes (pad rows). Each hit results in energy deposition in neighboring
pads. The total amount of the released energy, E, is a random
variable
with some p.d.f. f(E), 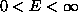 . The spatial distribution of the deposited energy among pads is bell-shaped,
say, a Gaussian, centered at the actual hit point
a with
a constant variance
. The spatial distribution of the deposited energy among pads is bell-shaped,
say, a Gaussian, centered at the actual hit point
a with
a constant variance 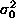 . The calculation gave
. The calculation gave
w(d;A)
= 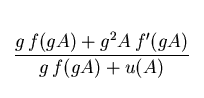 (1)
(1)
where 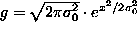 , u(A) is p.d.f. of a background amplitude A
measured in the given pad.
, u(A) is p.d.f. of a background amplitude A
measured in the given pad.
If the distribution f(E) is specified as an exponential
one with the mean 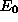 , i.e.
, i.e. 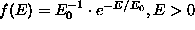 , then for a wide choice of the background component u(d)
(uniform or Gaussian with a wide
, then for a wide choice of the background component u(d)
(uniform or Gaussian with a wide 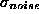 or even an exponential one with a large mean value in the cases of
or even an exponential one with a large mean value in the cases of  -electrons) we obtain quite an interesting 2D-weight ``surface'', see Fig.
2. For weak signals with a small amplitude
A the weight as
a function of the distance d has a ``bi-horn'' shape with
two pronounced peaks merging together when A is growing.
In a track-finding problem, this bimodal weight function is quite natural,
it indicates that weaker signals are less likely to appear in the closest
vicinity of the track line. Stronger signals are most likely to appear
right on the track line, hence the weight function has a narrow single
peak. Another problem appears in some experiments when in a certain pad
row all the signals are very weak. They will be all rejected by the bimodal
weight function, even though within that row the signals may have a nice
bell-shaped distribution with a local peak right on the track. In this
case one can apply a prior normalization of signals in each pad row in
a narrow corridor around the expected track line, see [7].
Lastly, in track-finding applications of bimodal weights to STAR TPC data,
we approximated nonlinear optimal weights by simple piece-wise linear functions
[7] (see fig. 2).
-electrons) we obtain quite an interesting 2D-weight ``surface'', see Fig.
2. For weak signals with a small amplitude
A the weight as
a function of the distance d has a ``bi-horn'' shape with
two pronounced peaks merging together when A is growing.
In a track-finding problem, this bimodal weight function is quite natural,
it indicates that weaker signals are less likely to appear in the closest
vicinity of the track line. Stronger signals are most likely to appear
right on the track line, hence the weight function has a narrow single
peak. Another problem appears in some experiments when in a certain pad
row all the signals are very weak. They will be all rejected by the bimodal
weight function, even though within that row the signals may have a nice
bell-shaped distribution with a local peak right on the track. In this
case one can apply a prior normalization of signals in each pad row in
a narrow corridor around the expected track line, see [7].
Lastly, in track-finding applications of bimodal weights to STAR TPC data,
we approximated nonlinear optimal weights by simple piece-wise linear functions
[7] (see fig. 2).
However, direct application of (1)
to the circle fitting using the pad raw data runs into two obstacles: (i)
it is very likely that some pads with a small amplitude appear right on
the fitted circle, see Fig. 1; (ii) the substantial
variability of photon energies distributed according to
f(x).
Both problems are solved in ref. [6] by ``integrating
away'' hidden parameters. The optimal weights have bimodal shape, but their
efficiency is lower due to disregarding some weak signals in areas between
clusters.
One more circle fitting problem relates to the frequent case of
several crossing circles. If one would fit them one by one, an extra data
contamination appears due to the influence of points of the ``stranger''
circle in the crossing area. So it would be more reasonable to fit those
circles simultaneously. For solving the problem of simultaneous fitting
of two or more circles it is necessary to create a single equation for
several circles. This is done in a way generalizing [8]
by multiplying the corresponding circle equations. The LSF estimation of
all parameters requires the search for the global minimum of the non-linear
functional 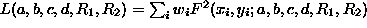 ,
where
,
where
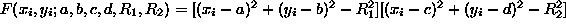 for two circles. A linearization of L is done similarly to ref.
[4]. Details can be found in ref. [9].
for two circles. A linearization of L is done similarly to ref.
[4]. Details can be found in ref. [9].
We tested the bimodal weight function in a numerical experiment and
compared it against two unimodal weights: Huber's [10],
Tukey's [11] and the constant one 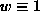 for the classical LSF. Results for the single circle experiment are summarized
in the table 1.
All rms values are given in bin-size, the half-width of the signal shape
is also equal to bin-size (
for the classical LSF. Results for the single circle experiment are summarized
in the table 1.
All rms values are given in bin-size, the half-width of the signal shape
is also equal to bin-size ( 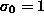 ). The noise distribution is uniform with signal/noise ratio = 1.
). The noise distribution is uniform with signal/noise ratio = 1.
| method |
Pf |
rmsa, b |
rmsR |
| LSF |
0.7570 |
0.231 |
0.420 |
| Huber |
0.1702 |
0.252 |
0.321 |
| Tukey (c = 4) |
0.0415 |
0.232 |
0.144 |
| Tukey (c = 3) |
0.0821 |
0.240 |
0.157 |
| bimodal |
0.0513 |
0.219 |
0.130 |
|
|
|
Table 1. Numerical characteristics of
three algorithms for circle fitting to simulated data. Here Pf
is the probability of a complete failure, when a and b
are off more than one bin size.
|
Only Tukey's unimodal biweight with c=4 stands the competition
with our bimodal one. The numerical results for two circles are shown in
the table 2. Simulation details can be found
in ref. [9].
| distance |
Pf |
rmsa, b |
rmsc, d |
| 1 |
0.0701 |
0.429 |
0.430 |
| 10 |
0.0474 |
0.333 |
0.390 |
|
|
|
Table 2. Numerical characteristics for
two circles fitting to simulated data using bimodal weights. Distances
are given in bin-size
|
Besides to be as close to real raw data as possible, a GEANT simulation
was made of pad structure for Cherenkov rings. We superimposed them into
the real background of the CERES Pb-AU'95 RICH data. Results of the ring
radius accuracy were comparable (not worse) than those presented in ref.
[4].



Next:3
Particle identificationUp:ContentsPrevious:1
Introduction
JINR
Elena Kolganova
1999-01-24




![]() . However, these violations often cause a complete breakdown of the LSF,
since data are contaminated by background measurements with p.d.f. u(d)
and, therefore
. However, these violations often cause a complete breakdown of the LSF,
since data are contaminated by background measurements with p.d.f. u(d)
and, therefore ![]() , where
, where ![]() and
and ![]() is the background rate. In such cases the robust weighted least
square procedure
is the background rate. In such cases the robust weighted least
square procedure ![]() works better. The optimal weight function
w(d) for
the uniform background distribution u(d) = const
was derived in our earlier papers [4, 6]
works better. The optimal weight function
w(d) for
the uniform background distribution u(d) = const
was derived in our earlier papers [4, 6]
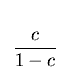
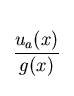
![]() . The spatial distribution of the deposited energy among pads is bell-shaped,
say, a Gaussian, centered at the actual hit point
a with
a constant variance
. The spatial distribution of the deposited energy among pads is bell-shaped,
say, a Gaussian, centered at the actual hit point
a with
a constant variance ![]() . The calculation gave
. The calculation gave
![]() for the classical LSF. Results for the single circle experiment are summarized
in the table 1.
All rms values are given in bin-size, the half-width of the signal shape
is also equal to bin-size (
for the classical LSF. Results for the single circle experiment are summarized
in the table 1.
All rms values are given in bin-size, the half-width of the signal shape
is also equal to bin-size ( ![]() ). The noise distribution is uniform with signal/noise ratio = 1.
). The noise distribution is uniform with signal/noise ratio = 1.