3 Particle identification

Considering the RICH detector as a part of a bigger experimental setup, we come to the natural assumption that the centers of Cherenkov rings and particle momenta are approximately known in advance from prior trajectory measurements. Therefore, the basic physical problem of particle identification reduces to making a decision about the most likely choice of a ring radius from two or three possible values. If the accuracy of those prior measurements is not sufficient enough, one can use them as initial values for the robust technique described in the previous section, in order to improve the ring parameter accuracy. It must be suitable for the well-known procedure of testing a hypothesis 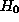 against an alternative hypothesis  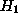. It consists in choosing a critical region  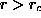on the basis of the likelihood ratio test (LRT). In the conventional formulation, when all hits on Cherenkov rings are determined and ring parameters are known, the corresponding LRT methods are well developed (see, e.g., ref. [1]). More popular are methods with counting the number of pads in fiducial areas calculated for alternative rings, as it was done in ref. [12]. Below we call such methods as PCFA (pad counting in fiducial area).
We propose a similar approach, but with calculating the sum of the amplitudes of pads occurred in a fiducial area around a tested circle. Since this sum should be much bigger for the circle corresponding to the true hypothesis than for the circle corresponding to the alternative hypothesis, the ratio of the first and the second sums must be greater than a chosen constant. Another argument that supports this test is as follows. It was noted in section 2, that the likelihood function can be expressed in terms of the weighted least squares with the optimally chosen weights. If we obtain from some previous calculations (or from other tracking detectors) sufficiently accurate circle center parameters, the weight function becomes constant equal to one in a narrow corridor around the circle and zero outside of that corridor, which is in fact the fiducial area for our ring. Therefore the likelihood function for raw data can be reduced to the sum of all amplitudes in this area. We played with various widths of the fiducial areas and found that the most effective is the narrowest one having the width of one pad size. Then we simulated Cherenkov pad structures corresponding to two various hypotheses of  and K particles with such momenta that corresponding distributions of Cherenkov radii overlapped. We check the basic hypothesis that a given particle belongs to the K family with smaller mean radius against the alternative hypothesis related to bigger mean radius.
 

a)	b)

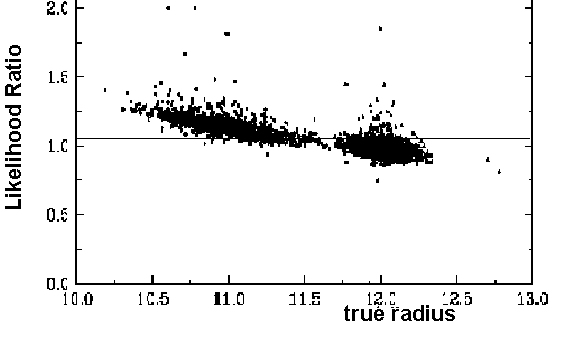
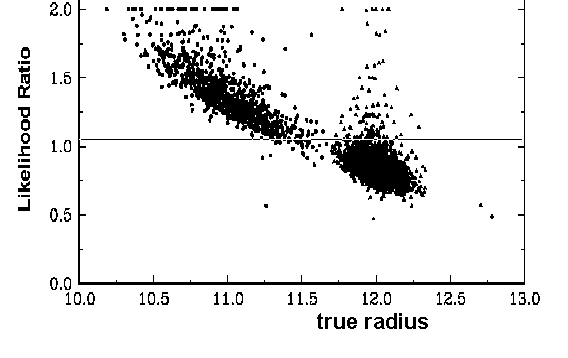
Figure 3: The likelihood ratio versus Cherenkov radius distribution. Application results of PCFA and ACFA methods shown in (a) and (b) correspondingly. On both pictures clouds correspond to two possible radii distributions, the upper cloud depicts the tested hypothesis. Horisontal line is set on LRT constant, hence the portion of the upper cloud lying under this line presents PID-errors, while the part of lower cloud lying above this line corresponds to cases of misidentification.
 

Results of our testing of both methods, PCFA and ACFA (amplitude counting in fiducial area), are presented in Fig. 3. The ACFA LRT constant was chosen to have the minimum PID-error probability (1.04%). Then we obtain the probability of ACFA misidentification equal to 2.4%, see fig.3b. For the PCFA method (see fig. 3a) the PID-error probability is three times worse: 3.2%, while the PCFA misidentification probability is almost on the same level as for ACFA: 2.3%.