N. Chernov
Department of Mathematics, University of Alabama,
Birmingham, AL 35294, USA
E. Kolganova and G. Ososkov
Laboratory of Computing Techniques and Automation,
Joint Institute for Nuclear Research,
Dubna, 141980 Russia
e-mail: kea@thsun1.jinr.dubna.su
The problem of approximating by a circle of measured data points, registered by modern detectors in high energy physics is considered. In this paper it's shown that the efficient way solve these problems of the curve fitting is the robust fitting technique based on a reweighted least square method with optimally chosen weights, obtained using the maximum likelihood approach. Results of a numerical experiment are demonstrate the high efficiency of the suggested method.
The problem of approximation of experimentally
measured points by circles is one of great
importance for data processing in high energy
physics. Various solutions have been developed
and proved efficient in many applications
[1, 2, 3].
This problem acquires a new twist, however, with the invention of such modern detectors as RICH (Ring Imaging CHerenkov) requiring in each event the reconstruction of tens and hundreds rings (circles) formed by Cherenkov photons. The novel feature of these detectors is their cellular, granular structure and discrete character of the experimental information. A typical RICH detector consists of a two-dimensional array (grid) of several thousands pads (cells). Each cell measures the energy released in it during the event.
The experimental information supplied by a RICH detector
is just an array of energies measured in the given cells.
This sharply contrasts with traditional track detectors
supplying an array of points 
making one or more circles (plus background). Now the cells
of a RICH detector with positive signals (measured energies)
can never make a perfect circle.
To allow an unambiguous reconstruction of a circle in a
single-photon hit RICH detectors are provided with a large
number of cells - 50,000 or more [4].
It is clear, however, that accurate reconstruction of
rings in RICH detectors requires brand new algorithms
for circle fitting. While traditional methods are based
on the random deviations of measured points 
from the real circle, now the cells are fixed but the
energy measurements have random character. Two more
features of cellular detectors should be noted also.
First, the energy dissipation produced by a hit by an
elementary particle results in positive signals in
several adjacent cells (a cluster), see fig. 1.
Second, the energy measured in cells is discretized and both
weak and too strong signals are cut off.
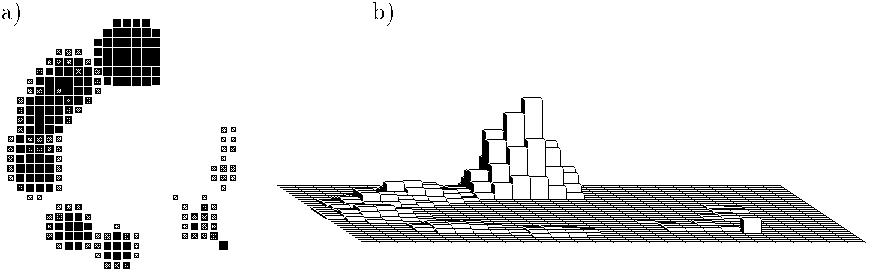
Figure: 2D (a) and 3D (b)
images of simulated discretized signals
of the same circle
Now a circle is to be fit to a few clusters of adjacent cells rather than to an array of individual points. The distribution of energy within cell and the cut-off rule for weak signals play crucial roles in the design of the circle-fitting techniques.
One should note that the high occupancy of RICH detectors
- the abundance of background hits and possible presense of
two or more overlapping rings require so called robust
algorithms to reduce noise sensitivity.
In this paper it is shown that efficient techniques of
circle fitting in cellular detectors are robust least
square procedures with optimally chosen weights.
Three problems are solved here:
As shown in [5], bimodal weight functions become optimal for
least square fit to signals measured by discrete, granular
detectors applying truncation rules for weak signals.
Intuitively, the value of the weight function w(x) can be interpreted
as a force by which the point at distance x from the fitting curve
`attracts' it.
In the `pure' classical least square fit (LSF) , all the data points are
`equally attractive' ( 
). The robust unimodal plateau-like
function makes all the points in a strip around the fitting curve
nearly equally attractive, and the rest neutral.
The logic is simple - the points in the strip belong to the track,
and the rest are just noise.
Bimodal weight functions, as compared to plateau-like ones, make the points on the sides of the main strip more attractive than those in the middle of the strip, leaving the points outside the strip neutral. An additional attracting force assigned to the points on the sides of the main strip (poorly fitted by the curve) gives the fitting curve better chances to adjust itself. It becomes more flexible and less likely to fall into a wrong local minimum of the function. Our numerical experiment reported below demonstrates the advantages of bimodal weight functions over various unimodal and plateau-like ones.
As it was pointed out, any kind of data contaminations can distort considerably estimations of the circle center or radius. This effect is especially specific for several crossing circles, if you would fit them one by one because of the influence of points of the "stranger" circle from the crossing area. So we have to fit both circles simultaneously.
For solving the problem of simultaneous fitting of two or more circles it is necessary to create the equation of such a combined curve. It can be done in a way generalizing [9] by multiplying the corresponding number of the circle equations. The LSF estimation of all parameters requires the search for the global minimum of the non-linear functional
We linearize the problem assuming that the distances
of the initial values of our parameters from the
exact values of corresponding parameters are so small that any of their
products or squares are negligible. Then we differentiate the functional
(1) by parameters 
and substitute each
parameter by the sum of its initial value and corresponding delta-correction.
Omitting all members of the second order of smallness and higher we convert
the obtained non-linear equations to the normal system of linear equations.
So its minimization is not a complicate problem. Adding
obtained corrections to the initial values of parameters we repeat the whole
procedure iteratively until the corrections become less than a prescribed
value or the number of iterations attains its limits.
We have tested the bimodal weight functions in a computer experiment. Here we report the results. The data have been simulated as discribed in [5]. A typical data sample in this experiment is histogrammed and shown on Fig. 1. Here the height of a bar over a cell represents the amplitude of energy measured in it.
The simulated data are then fit by a circle through weighted least square procedure using known easy algorithm [1]. The initial circle is picked randomly, with centers about two cells off the the actual values of coordinates a,b and radius of circle r . This is a pretty bad approximation, but these values are typical. Then the iterative procedure works until convergence, but not longer than 10 iterations.
The quality of the algorithm is characterized by three
parameters. The first is the probability 
of a complete
failure, which occurs if the estimated values of
a and b are off by 
(here 1 is the size of a cell)
or the estimated value of R is off by 
. The other two
characteristics are the root mean square error
in the estimates of a and b, denoted by 
,
and the same error in R, denoted by 
. The values of
and are computed based on non-failing runs only
(in the above sense).
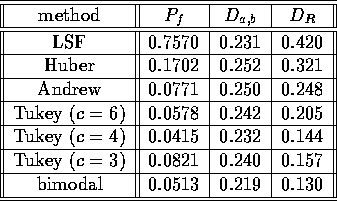
Table 1: Numerical characteristics of four algorithms
for circle fitting to simulated data.
The weights 
were computed by various methods. We
tried both unimodal and bimodal weight functions. Three unimodal
functions we tested were famous Huber's function [6],
Tukey's biweights [7], and Andrews's sine [8].
We tested various simple (piecewise linear) approximations to
the bimodal optimal weight functions found in [5].
The following one was the most successful:
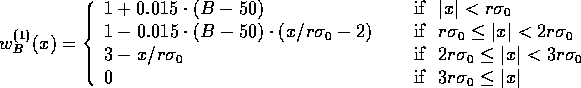
were r=1-B/200 and B is amplitude of signal.
The numerical results of our single circle experiments are summarized in the table 1. Only Tukey's unimodal biweight with c=4 stands the competition to some extent, other unimodal functions are clearly poorer than our bimodal one. The first line corresponding to the non-weighted least square fit is included just to demonstrate the necessity of robust algorithms for accurate processing of noisy data.
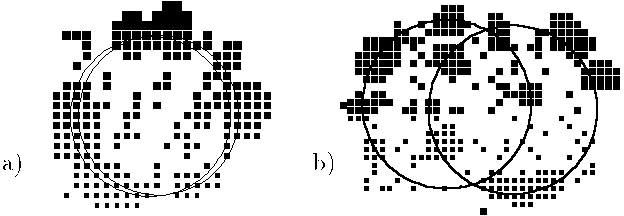
Figure 2: The result of fitting the simulated discretized signals of two
circles, a) distance between circles - 1, b) - distance 10.
The data of two circles have been simulated by the same way as one circle. The second circle has the same radius as the first one and is shifted from it along axes OX, d = b . The initial circles are picked randomly, with centers about one cells off the the actual values of a,b,c,d . The radius of circles is fixed. A typical data sample in this experiment is histogrammed and shown on Fig. 2. The numerical results are shown in the table 2.
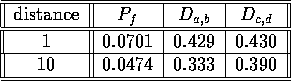
Table 2: Numerical characteristics for two circuls fitting
to simulated data using bimodal weights.
